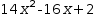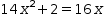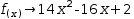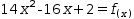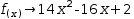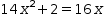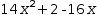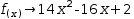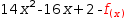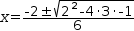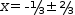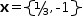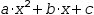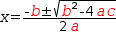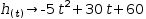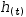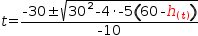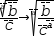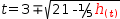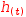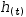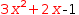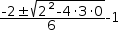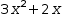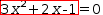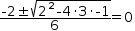3.4.5 Quadratic

Quadratic transforms an expression by applying the quadratic formula. Normally the transformation applies to the entire active expression which must adhere to one of the following criteria.

• a formula containing a binomial; example: 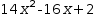14⋅x^2-16⋅x+2
• an equation containing a binomial; example: 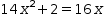14⋅x^2+2=16⋅x
• a function definition with a single parameter and a binomial elaboration; example: 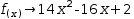f(x)→14⋅x^2-16⋅x+2

3.4.5.1 Finding roots

The quadratic formula is used to find the roots of a binomial equation. The following pretransformations are applied to extract a suitable binomial from the active expression.

• If an equation contains a zero on either side, the binomial is taken from the other side.
• If an equation contains a function expression on either side it is treated like a function definition with a left-right exchange where appropriate; example: 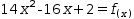14⋅x^2-16⋅x+2=f(x) is treated like 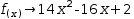f(x)→14⋅x^2-16⋅x+2.
• Any other equation is transformed into a formula by subtracting the left side from the right side; example: 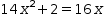14⋅x^2+2=16⋅x is treated like 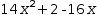14⋅x^2+2-16⋅x
• The elaboration of a function definition is transformed into a formula with the function part wrapped in a guard and subtracted from the elaboration; example: 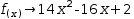f(x)→14⋅x^2-16⋅x+2 is transformed into 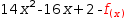14⋅x^2-16⋅x+2-.[f(x)]

For example, Quadratic transforms 3⋅x^2+2⋅x-1=0 to 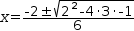x=(-2±√(2^2-4⋅3⋅-1))÷6, which simplifies to 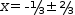x=-(1/3)±2/3. After distributing the right side and simplifying the expression becomes 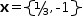xʂ={1/3, -1}, an expression that equates the set xʂ with a set containing two scalars representing the roots of x.

The expression 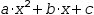a⋅x^2+b⋅x+c does not meet the criteria for the quadratic transformation because it represents a function of four variables. However, by protecting the coefficients (see §3.3.2), the expression is transformed to 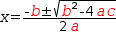x=(-.[b]±√(.[b]^2-4⋅.[a]⋅.[c]))÷(2⋅.[a]).

A protected function definition combined with its elaboration is useful in discovering inverse functions. Since the function part is wrapped in a guard, it is included in the c term of the quadratic expression. For example, the height of a ball at time t thrown upwards and outwards from an initial height of 60 meters is given by 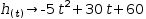h(t)→-5⋅t^2+30⋅t+60. The inverse function answers the question: given a height, at what point in time will the ball reach that height? That is, we need to solve for t in terms of 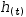h(t). The quadratic transform produces 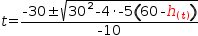t=(-30±√(30^2-4⋅-5⋅(60-.[h(t)])))÷-10, which ultimately simplifies (with the aid of 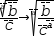ʈroot(a, b)÷c→root(a, b÷c^a))to 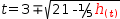t=3∓√(21-1/5⋅.[h(t)]). For this expression, supplying a value for 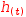.[h(t)] and evaluating provides an answer for the inverse function: given a height, at what point in time will the ball reach that height. (Since the ball rises and then falls, there are two answers to this question and a useful solution requires 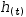h(t) to be constrained to certain intervals.)

3.4.5.2 Variation

There is an exception to the formula rule given above: a portion of a formula can be selected and converted to a quadratic. Thus 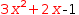.[3⋅x^2+2⋅x]-1 and Quadratic becomes 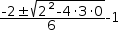(-2±√(2^2-4⋅3⋅0))÷6-1. Note the transformation results ultimately in {-1, -(5/3)}, which represents the roots of 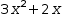3⋅x^2+2⋅x diminished by 1. This illustrates that Quadratic applied indiscriminately can produce misleading results. Pursuing this line of thinking, consider what would happen if Quadratic was applied just to the selected left side in 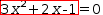.{3⋅x^2+2⋅x-1}=0. If this was allowed, the transformation would produce 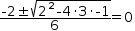(-2±√(2^2-4⋅3⋅-1))÷6=0. After additional transformations, it can be seen that the resulting -(1/3)±2/3=0 is a contradiction. For this reason, Myron does not permit Quadratic to be applied to subexpressions of equations or definitions. The exception for subexpressions of formulae is for convenience and is allowed because it does not lead to contradictions.